Quelques
problèmes
pour lesquels il faut penser différemment de ce que l'on a l'habitude de le faire...
Quelques
problèmes
pour lesquels il faut penser différemment de ce que l'on a l'habitude de le faire...
Un homme qui aimerait bien être heureux marche sur un chemin.
Après quelque temps, il rencontre un sage qui lui dit : "Plus loin, le chemin se divise en deux parties ; l’une mène au bonheur, l’autre au malheur et tu ne pourras pas revenir sur tes pas. L’embranchement est gardé à tour de rôle par deux frères.
Tous deux savent où se trouve le bon chemin ; mais l’un dit toujours la vérité et l’autre ne peut que mentir. On ne sait jamais si l’on a devant soi le menteur ou celui qui dit la vérité.
Quelle question devras-tu poser à celui que tu rencontreras pour trouver le bon chemin ?
Tu n’auras droit qu’à une seule question !"
Grand classique des énigmes du genre pseudo-paradoxe, celle-là est un formidable casse-tête. La bonne question tient en une seule phrase !
On dispose de 5 chapeaux : 3 blancs et 2 noirs.
3 personnes sont alignées l'une derrière l'autre; elles ne connaissent pas la couleur de leur chapeau.
- Le dernier voit les 2 premiers et dit : je vois la couleur de vos chapeaux, mais je ne connais pas la mienne!
- Le deuxieme voit la couleur du premier et dit : je ne connais pas la mienne!
- Le premier dit : j'ai deviné la couleur de mon chapeau !
Question: quelle est la couleur du chapeau du premier ?
Comment tracer un cercle et son axe sans lever son stylo?
(Bien sûr, les deux ne doivent pas être reliés par un trait...) Si, c'est vraiment possible !!!
Rejoignez les neuf points qui composent ce carré avec seulement 4 droites continues...(toujours sans lever la pointe du stylo)
* * *
* * *
* * *
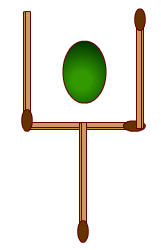
- Avec des allumettes : recréez exactement le même symbole (composé de 4 allumettes) que celui ci dessous mais l'objet placé à l'intérieur (une olive...) doit se retrouver en dehors du symbole. Pour cela vous ne devez déplacer que deux allumettes.
